Product Exhaustion Theorem of Euler and Clark (With Diagram)

History of Product Exhaustion Theorem

The Product Exhaustion Theorem has its roots in the early works of classical economists such as Adam Smith and David Ricardo. These economists recognized that consumers faced budget constraints and had to choose how to allocate their limited resources between different products.

However, the Austrian economist Carl Menger developed the concept of marginal utility in the late 19th century. Menger argued that the value of a good or service is determined by its marginal utility, which is the additional satisfaction or utility that a consumer derives from consuming one more unit of the good or service.

Building on Menger’s work, the Product Exhaustion Theorem was further developed by other economists, such as William Jevons and Alfred Marshall, in the late 19th and early 20th centuries. These economists recognized that consumers would continue to consume a product until its marginal utility fell to zero and then move on to consuming other products.

Understanding Product Exhaustion Theorem

In economics, there exists a principle known as the Product Exhaustion Theorem. This principle is crucial as it helps explain consumers’ behaviour in the market, particularly concerning their consumption patterns.

The Product Exhaustion Theorem is based on the assumption that consumers have a fixed budget or income that they can use to purchase goods and services. Given this budget constraint, consumers must choose how to allocate their limited resources between the available products. The theorem states that if the consumer continues to consume a product until the marginal utility of the product falls to zero, then the consumer has exhausted the product.

To understand this theorem better, let us take an example. Suppose a consumer has a budget of Rs. 100, and two products are available in the market, Product A and Product B. The consumer can choose to allocate his/her budget between the two products in any manner. Suppose the consumer decides to spend Rs. 50 on Product A and Rs. 50 on Product B.

Now, according to the Product Exhaustion Theorem, the consumer will continue to consume Product A until the marginal utility of the product falls to zero. This means that the consumer will keep buying and consuming Product A until he/she no longer gains additional satisfaction or utility. Once the marginal utility of Product A falls to zero, the consumer will move on to consuming Product B and will continue to do so until the marginal utility of Product B falls to zero as well.

The Product Exhaustion Theorem helps to explain why consumers tend to consume more of certain products than others. Consumers will continue to consume a product until they have exhausted its marginal utility and then move on to consuming other products. This behaviour is limited to individual consumers and observed at a macro level, where entire economies may experience product exhaustion.

For instance, during the early stages of industrialization, many countries relied heavily on the export of primary commodities such as agricultural products, minerals, and natural resources. However, as these economies developed, they began to experience product exhaustion. The marginal utility of these primary commodities began to fall, and the economies had to shift towards producing and exporting more value-added products to sustain their economic growth.

Euler’s Product Exhaustion Theorem: Understanding the Theory of Distribution

In economics, the theory of distribution plays a crucial role in understanding how the total output of a production process should be allocated among the different factors of production. The Product Exhaustion Theorem, developed by the Swiss mathematician Leonhard Euler in the eighteenth century, provides a solution to this question by demonstrating how payments to the factors of production can exactly exhaust the total product.

According to the Product Exhaustion Theorem, since each factor of production is rewarded equal to its marginal product, the total product will eventually be exhausted. In other words, the theorem states that in a competitive factor market, when every factor employed in the production process is paid the price equal to the value of its marginal product, payments to the factors will exactly exhaust the total value of the product.

The adding-up problem, also known as the Wicksteed problem, provides a way to demonstrate this proposition. It can be shown numerically that the total output (Q) is equal to the sum of the marginal product of labour (MP_L) and the marginal product of capital (MP_C) multiplied by their respective prices (P). Therefore, the total value of the output (PxQ) is equal to the sum of the value of the marginal product of labor (VMP_L) and the value of the marginal product of capital (VMP_C).

Euler’s theorem suggests that the total production should be distributed among the different factors of production in proportion to their marginal product. This means that the factor contributing the most to the production process should receive the highest reward. Furthermore, the theorem suggests that a firm should employ its inputs to the extent to which the reward to the factor equals its marginal revenue product.

Mathematical interpretation of Euler’s Product Exhaustion Theorem

Euler’s Product Exhaustion Theorem is a mathematical principle that explains how payments to the factors of production can exactly exhaust the total product. The theorem is based on the assumption of perfect competition and constant returns to scale and relies on marginal productivity.

Mathematically, the theorem can be expressed as:

Q = f(L,K)

Where

Q is the total output of the production process,

L is the labour employed,

K is the capital employed, and

f(.) is a production function that relates the inputs to the output.

Assuming that the production function is homogeneous of degree one (i.e., doubling the inputs doubles the output), Euler’s theorem states that:

rL = MP_L

rK = MP_K

Where

rL and rK are the rental rates of labour and capital, respectively, and

MP_L and MP_K are the marginal products of labour and capital, respectively.

The rental rates represent the payments made to the factors of production, and the marginal products represent the additional output produced by an additional unit of input. According to the theorem, the rental rates must equal the marginal products to exhaust the total product. In other words, the sum of the payments made to the factors of production must equal the total output of the production process.

Mathematically, this can be expressed as:

rL x L + rK x K = Q

or

VMP_L + VMP_C = PQ

Where

VMPL and VMPC are the value of the marginal product of labour and capital, respectively, and

P is the price of the output.

Euler’s Product Exhaustion Theorem provides a mathematical interpretation of the theory of distribution and offers a way to allocate the total product among the different factors of production. The theorem implies that the relative productivity of the different factors of production determines the income distribution in an economy. It solves the producer’s long-run problem of allocating the total product to each factor and distributing the total outlay among the different inputs.

Importance of Euler’s Product Exhaustion Theorem

1. Allocation of resources: Euler’s theorem provides a mathematical framework for allocating resources among the different factors of production. The theorem implies that the relative productivity of the different factors of production determines the income distribution in an economy. It solves the producer’s long-run problem of allocating the total product to each factor and distributing the total outlay among the different inputs.
2. Efficiency: By allocating resources based on the marginal productivity of factors, Euler’s theorem provides a way to ensure that resources are used efficiently. The theorem suggests that firms should employ their inputs to the extent to which the reward to the factor equals its marginal revenue product.
3. Long-run equilibrium: The theorem provides a way to understand long-run equilibrium in a perfectly competitive market. According to the theorem, in long-run competitive equilibrium, price equals minimum average cost, and the firm’s cost curve at that point is horizontal.
4. Price determination: Euler’s theorem explains how prices are determined in a perfectly competitive market. The theorem implies that prices will be set based on the marginal productivity of factors and that prices will adjust until they equal the marginal revenue product of each factor.

Criticisms/ Limitations of Euler’s Product Exhaustion Theorem

1. Constant returns to scale: Euler’s theorem assumes constant returns to scale, which may not be realistic in the real world. In practice, many firms may operate at increasing or decreasing returns to scale.
2. Perfect competition: The theorem assumes perfect competition, which may not be realistic in many markets. In practice, many markets are imperfectly competitive, with a few firms dominating the market.
3. Labour-capital dichotomy: The theorem assumes a dichotomy between labour and capital, which may not accurately reflect the diversity of factors of production. In practice, there may be many other factors of production, such as land, natural resources, and technology.
4. Distributional implications: The theorem has distributional implications that may not be desirable from a social perspective. For example, the theorem implies that those more productive factors will receive a larger share of the total output, regardless of their contribution to society. This may lead to inequality and social unrest.

Clark’s Production Exhaustion Theorem

Clark’s Production Exhaustion Theorem is an essential principle in economics that helps to explain the distribution of income among the different factors of production. The theorem was developed by John Bates Clark, an American economist who lived from 1847 to 1938. Clark was a professor of economics at Columbia University and made significant contributions to the field of economics, particularly in labour economics and distribution theory.

Clark’s Production Exhaustion Theorem was introduced in his book “The Distribution of Wealth” in 1899. The theorem builds on the classical economists’ concept of marginal productivity. It asserts that in a perfectly competitive market, each factor of production will be rewarded with a share of the total output equal to its marginal product. This, in turn, leads to the exhaustion of the total product.

Assumptions of Clark’s Production Exhaustion Theorem

Clark’s Production Exhaustion Theorem makes several assumptions about the market and the behaviour of firms and workers. These assumptions include the following:

1. Perfect competition: The theorem assumes that the market is perfectly competitive, with many buyers and sellers, no barriers to entry or exit, and perfect information.
2. Homogeneous inputs: The theorem assumes that all inputs are homogeneous, meaning that they are identical in quality and can be substituted for one another without affecting the final product.
3. Marginal productivity: The theorem is based on the concept of marginal productivity, which assumes that the productivity of each input is determined by the number of other inputs used in the production process.
4. Diminishing marginal productivity: The theorem assumes that the marginal productivity of each input decreases as more of it is used in the production process.
5. Profit maximization: The theorem assumes that firms are profit maximizers and will hire inputs up to the point where the marginal product of each input is equal to its price.

Explanation of Clark’s Production Exhaustion Theorem with Diagram

According to Clark’s Production Exhaustion Theorem, in a perfectly competitive market, each factor of production will be rewarded with a share of the total output equal to its marginal product. This means the price paid for each input will equal the value it contributes to the final product. In other words, each input will be rewarded in proportion to its contribution to the total output.

Clark’s Production Exhaustion Theorem explains the distribution of the total product in an economy with two factors of production: labour and capital. The theorem assumes that labour and capital are the only factors of production and that the production function is characterized by diminishing marginal returns.

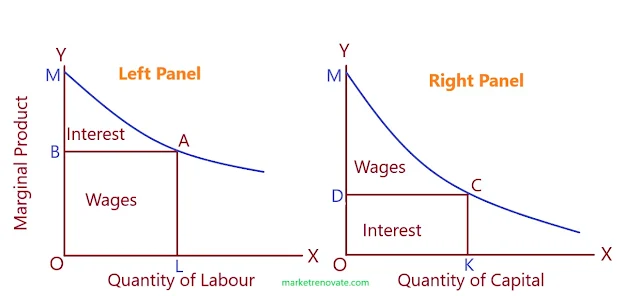
Clark summarized the workings of this economy in a diagram where the horizontal axis represents the units of labour or capital, and the vertical axis represents the marginal physical product of labour or capital.

We can explain Clark’s Production Exhaustion Theorem with the help of the following diagram:

In the left panel of the diagram, the MPL curve shows that as more workers are employed with fixed capital, the marginal physical product of labour falls steadily. The OL line represents the number of workers available for employment. If all workers are employed, the last worker is paid LA wage, and the total wage bill is the number of workers OL multiplied by the wage rate LA. The triangular area ABM goes to the owners of capital as the residual interest. Thus, the two economic factors fully distribute the total product between labour and capital.

In the right panel of the diagram, if labour is a fixed factor and capital is a variable factor in the economy, it can again be shown that the total product is fully exhausted. The MPc curve shows that given the same quantity of labour OK, capital is employed with KС as its marginal product, so the interest rate is OD = KС per unit of capital. The workers receive wages equal to the area CDM. Thus, the total product of the economy is fully distributed between owners of capital as interest equal to the area OKCD and workers as wages equal to the area CDM, so that ОМСK = OKCD + CDM.

Criticisms of Clark’s Production Exhaustion Theorem

Some of the main criticisms of J.B. Clark’s Product Exhaustion Theorem include the following:

1. Unrealistic assumptions: Clark’s theorem relies on several assumptions that may not hold in real-world economies. For example, the assumption of perfect competition may not always hold, and factors of production may not be equally mobile or homogeneous.
2. Ignores externalities: The theorem does not account for externalities, which can significantly affect the total product distribution between labour and capital. For example, pollution or resource depletion can affect the product’s value.
3. Limited to static analysis: The theorem is limited to static analysis of the economy and does not account for changes over time. In reality, economies are dynamic and subject to constant change.
4. Oversimplifies complex systems: Clark’s theorem oversimplifies the complex interactions between labour and capital and the distribution of income and wealth. These factors are influenced by various social, political, and economic factors that cannot be reduced to a simple diagram.